Lesson09 グラフを描く

前回の復習
前回出た重要キーワード
- for ループ変数(要素)in リスト の構文
- for インデックスの番号 ,それに対応するリストの中身 enumerate(リスト) の構文
- リストの要素がリストのときの要素のアクセス方法
- 要素が数値のリストの最大値、最小値を求める max , min 関数の使い方
- fruits = [‘りんご’,’みかん’,’バナナ’] という配列でfor f in fruits というループと for k in range(0,4) という書き方はどのような違いがあるか思い出しましょう。
1グラフの描き方
この章のキーワード
- 散布図
- プロット
- import matplotlib.pyplot as plt でグラフを描く方法
1.1 散布図のグラフ
次のような5組のデータがあったとします。
(x, y) = (1, 2), (2, 4), (3, 6), (4, 8), (5, 10)
このデータをグラフにしてみましょう。xy 平面に点としてプロットしてみます。
まず、x, y をそれぞれ別のリストにします。
1 2 |
X = [ 1, 2, 3, 4, 5 ] y = [ 2, 4, 6, 8, 10 ] |
|---|
次に、下のグラフの描き方に従って、散布図をプロットします。
散布図の描き方
import matplotlib.pyplot as plt #この行はそのまま構文として暗記しましょう x = X座標のリスト y = Y座標のリスト plt.scatter(x,y) #この行はそのまま構文として暗記しましょう plt.show() #この行はそのまま構文として暗記しましょう
x, y は好きな変数にできます。
一般に、 x と y あるいは X と y にします。なぜ X だけが大文字かというと、高校で学習する行ベクトルという意味合いがあります。
これをもとに、上のデータをグラフ化するコードを書いてみます。
lesson_0009_10.py
1 2 3 4 5 |
import matplotlib.pyplot as plt X = [ 1, 2, 3, 4, 5 ] y = [ 2, 4, 6, 8, 10 ] plt.scatter(X,y) plt.show() |
|---|
実行結果
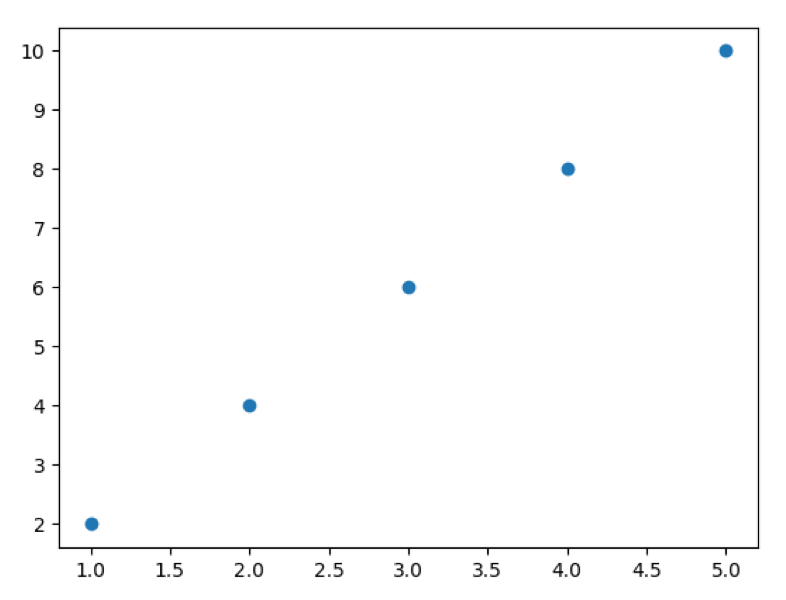
軸の長さや目盛りの刻みは自動的に Python が設定してくれます
1.2 線で結ぶ
いわゆるグラフを描くこともできます。plot という関数を使います。
| 1 | plt.scatter(X,y) |
|---|
が
| 1 | pplt.plot(X,y) |
|---|
に変わっただけです。
lesson_0009_20.py
1 2 3 4 5 |
import matplotlib.pyplot as plt X = [ 1, 2, 3, 4, 5 ] y = [ 2, 4, 6, 8, 10 ] plt.plot(X,y) plt.show() |
|---|
実行結果
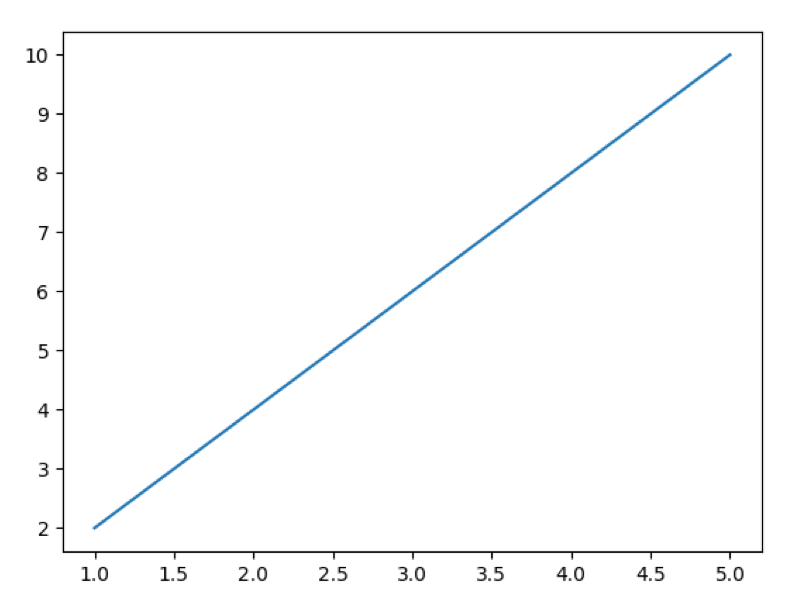
点もプロットしたければ、scatter と plot の両方の命令を書きます。
1 2 |
plt.scatter(X,y) plt.plot(X,y) |
|---|
すなわち、
1 2 3 4 5 6 |
import matplotlib.pyplot as plt X = [ 1, 2, 3, 4, 5 ] y = [ 2, 4, 6, 8, 10 ] plt.scatter(X,y) plt.plot(X,y) plt.show() |
|---|
実行結果
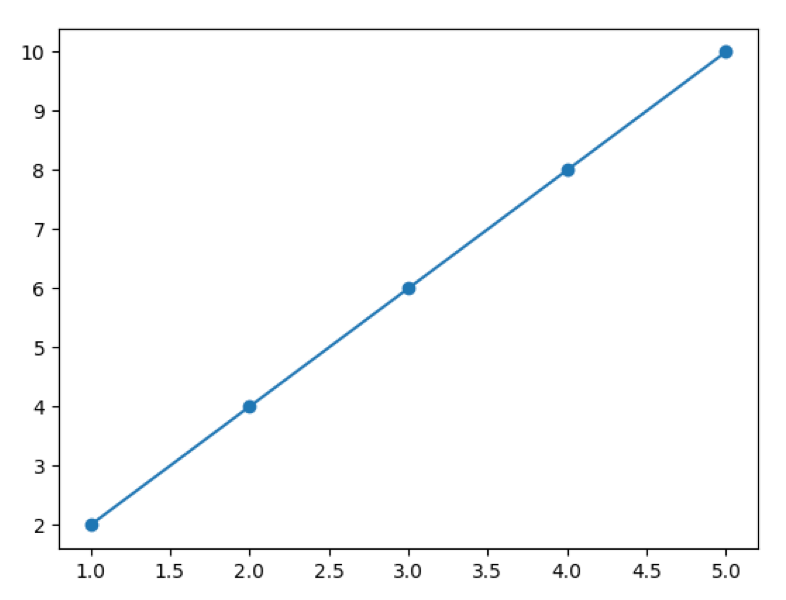
一般的に工学分野でグラフを描写する場合、グラフにするデータは、ある時点で観測した値、また次の時点で観測した値、、、のように、連続でないデータになります。線でむすんでいるところは、あくまでも実際の観測データから予想している補完された値ということを忘れないでください。
2 つのデータをそれぞれ描くには、2 組の x, y のリストを用意します。
lesson_0009_30.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import matplotlib.pyplot as plt X1 = [ 1, 2, 3, 4, 5 ] y1 = [ 2, 4, 6, 8, 10 ] X2 = [ 1, 2, 3, 4, 5 ] y2 = [ 1.5, 3.0, 4.5, 6.0, 7.5 ] plt.scatter(X1,y1) plt.plot(X1,y1) plt.scatter(X2,y2) plt.plot(X2,y2) plt.show() |
|---|
実行結果
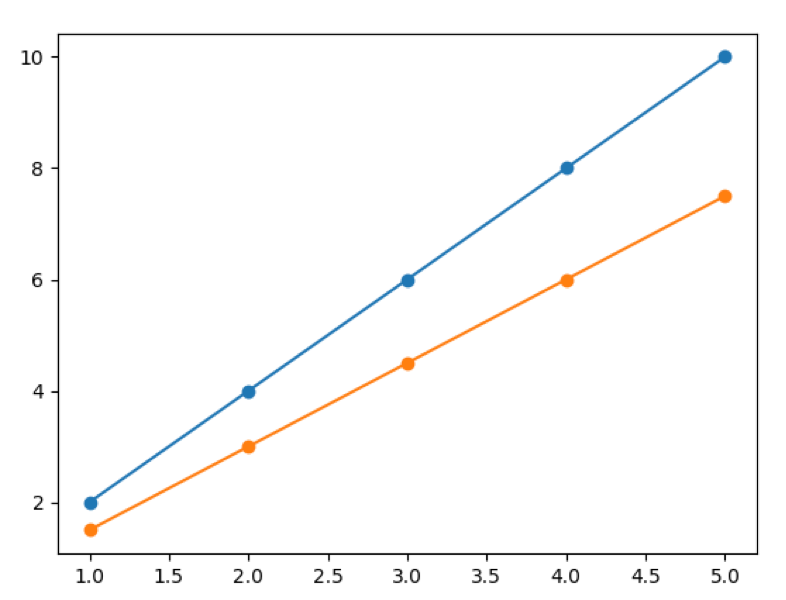
1.3 数学の関数を描く
数学の関数を描くこともできます。数学の勉強に役に立ちますね。
数学関数の描き方( 1 変数)
import matplotlib.pyplot as plt import numpy as np x = np.linspace( グラフ横軸最小値, グラフ横軸最大値, 分割程度) y = x で関数を表現する plt.plot(x, y) plt.show()
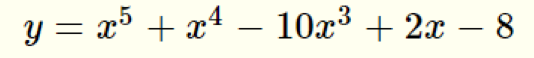 のグラフを描いてみましょう。
のグラフを描いてみましょう。
lesson_0009_40.py
1 2 3 4 5 6 |
import matplotlib.pyplot as plt import numpy as np x = np.linspace( -4, 3, 70) y = x**5 + x**4 -10*x**3 + 2*x -8 plt.plot(x, y) plt.show() |
|---|
| 1 | x = np.linspace( -4, 3, 70) |
|---|
の部分について解説しましょう。これは、x 軸の範囲を示します。1 つ目の引数が x の最小値、次が x の最大値です。最後の引数 70 はどれだけ細かく分割しているかということを表しています。グラフも滑らかに見えて実は散布図の点と点の間を直線で結んでいるだけです。この数字が大きければ大きいほど滑らかになります。ためしに荒くしてみましょう。
lesson009_50.py
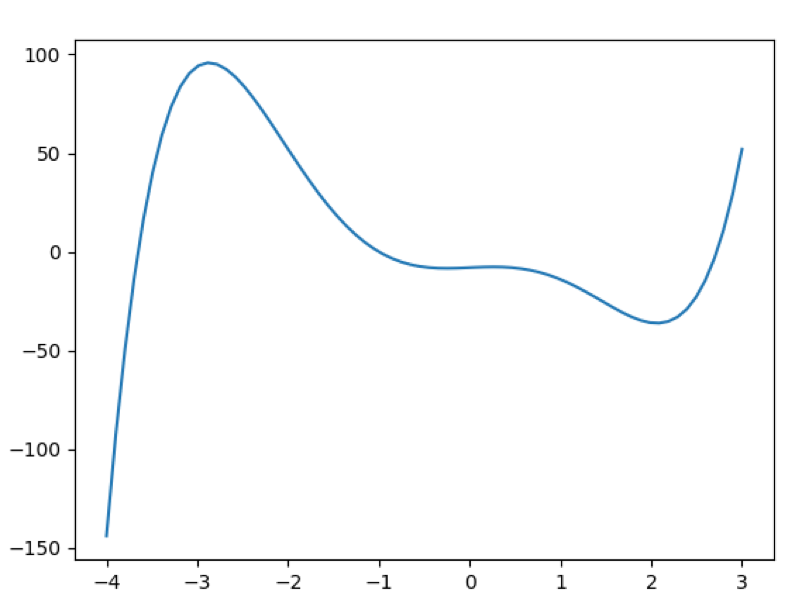
| 1 | x = np.linspace( -4, 3, 10) |
|---|
このようにガタガタになりました。
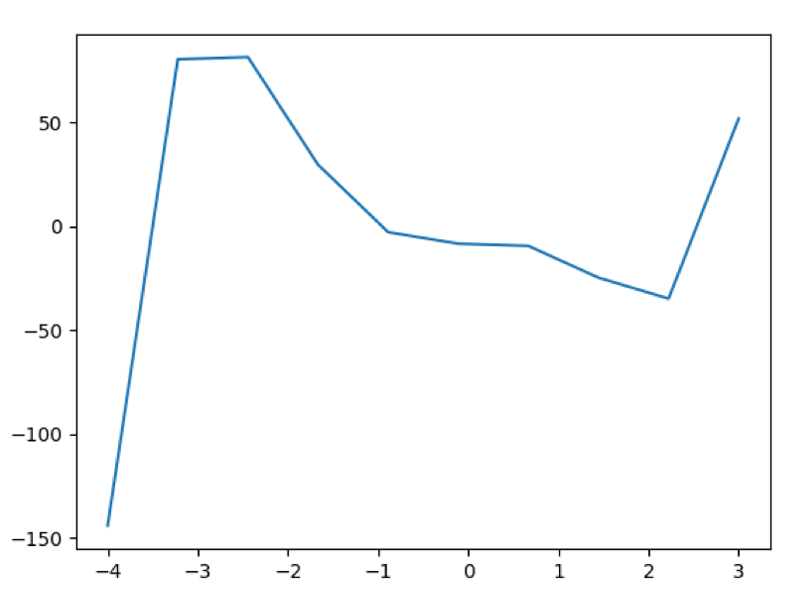
グラフを描くとデータが可視化され、わかりやすくなります。世の中のグラフは何かを観測した結果がほとんどなので、散布図でまずデータを可視化し、それから様々な仮説を入れたり、予想したりしていきます。
演習の時間
演習の解答はここからダウンロードできます。ダウンロードfile_download
演習1
A 子さんはアサガオの種5 個をまいて、そのそれぞれ発芽からの日数と背丈の高さを調べました。下の表はこれをまとめたものです。この表を使ってこの観察記録について考えてみましょう。
A 子さんのアサガオの発芽からの背丈
| 個体1 | 個体2 | 個体3 | 個体4 | 個体5 | 平均 | |
|---|---|---|---|---|---|---|
| 2日目 | 1.4 | 1.5 | 1.6 | 1.7 | 1.7 | |
| 3日目 | 2.5 | 2.4 | 2.1 | 2.8 | 2.9 | |
| 4日目 | 3.2 | 3.3 | 3.5 | 3.6 | 3.6 | |
| 5日目 | 3.8 | 4 | 4.1 | 4.5 | 4.4 | |
| 6日目 | 4.5 | 4.7 | 4.8 | 5.2 | 5.3 | |
| 7日目 | 5.5 | 5.6 | 5.7 | 6 | 6.2 | |
| 8日目 | 6.1 | 6.1 | 6.2 | 6.8 | 7.1 |
上のデータを次のようなリストにしました。
asagaoA.py
1 2 3 4 5 6 7 8 9 |
asagaoA = [ [1.4, 1.5, 1.6, 1.7, 1.7], [2.5, 2.4, 2.1, 2.8, 2.9], [3.2, 3.3, 3.5, 3.6, 3.6], [3.8, 4, 4.1, 4.5, 4.4], [4.5, 4.7, 4.8, 5.2, 5.3], [5.5, 5.6, 5.7, 6, 6.2], [6.1, 6.1, 6.2, 6.8, 7.1], ] |
|---|
(1)発芽第 N 日目の 5 つのアサガオの平均を求めて、上の表を埋めてください。
具体的には、計算は電卓や暗算ですることなく、上のデータを使って Python で平均値のリストを作って下さい。このとき、sum 関数を使うと便利です。sum は、リストの要素が数字であればそれを足す関数です。 例:sum([ 1,2,3,4]) は 10 を返します。
アサガオの平均値
| 5つのアサガオの平均 | |
|---|---|
| 2日目 | 1.58 |
| 3日目 | 2.54 |
| 4日目 | 3.44 |
| 5日目 | 4.16 |
| 6日目 | 4.9 |
| 7日目 | 5.8 |
| 8日目 | 6.46 |
(2) A子さんのアサガオの平均値を横軸に発芽日数、縦軸に背丈の高さにしてグラフにしてみましょう。
(3) (2)のグラフからこの 5 つのアサガオの 10 日後の平均は、何センチくらいか予想してみましょう。
大人のあなたへ
演習1の(3)は、ほぼ直線にのっているデータから、そのデータの直線の方程式を求めるという問題が背景にあります。その直線が分かれば計測できない未知のxに対応するyの値を予測できるのです。
データサイエンスの重要な役割は、自身が収集できる限りあるデータからそのデータの振る舞いを解析し、未来を予想することです。
この問題はデータサイエンスの初めの一歩に当たるかもしれません。
さて、この直線を決定する代表的な方法として「全データの誤差が最小になる」ように決定する回帰直線と呼ばれるものがあります。
この回帰直線の傾きと切片を求めるには、高校の数学で学習する平方完成を使うと計算できますが、興味のある人はインターネット等で調べてPythonのソースコードにしてみましょう。なお、ダウンロード用のソースに参考として入れています(enshu0009_03_sanko.py)。
何をもって「誤差」とするかといった興味深い問題です。
また、scikit-learnというモジュールを使うと、もっと簡単にこの直線を決定することができます。
